Publications

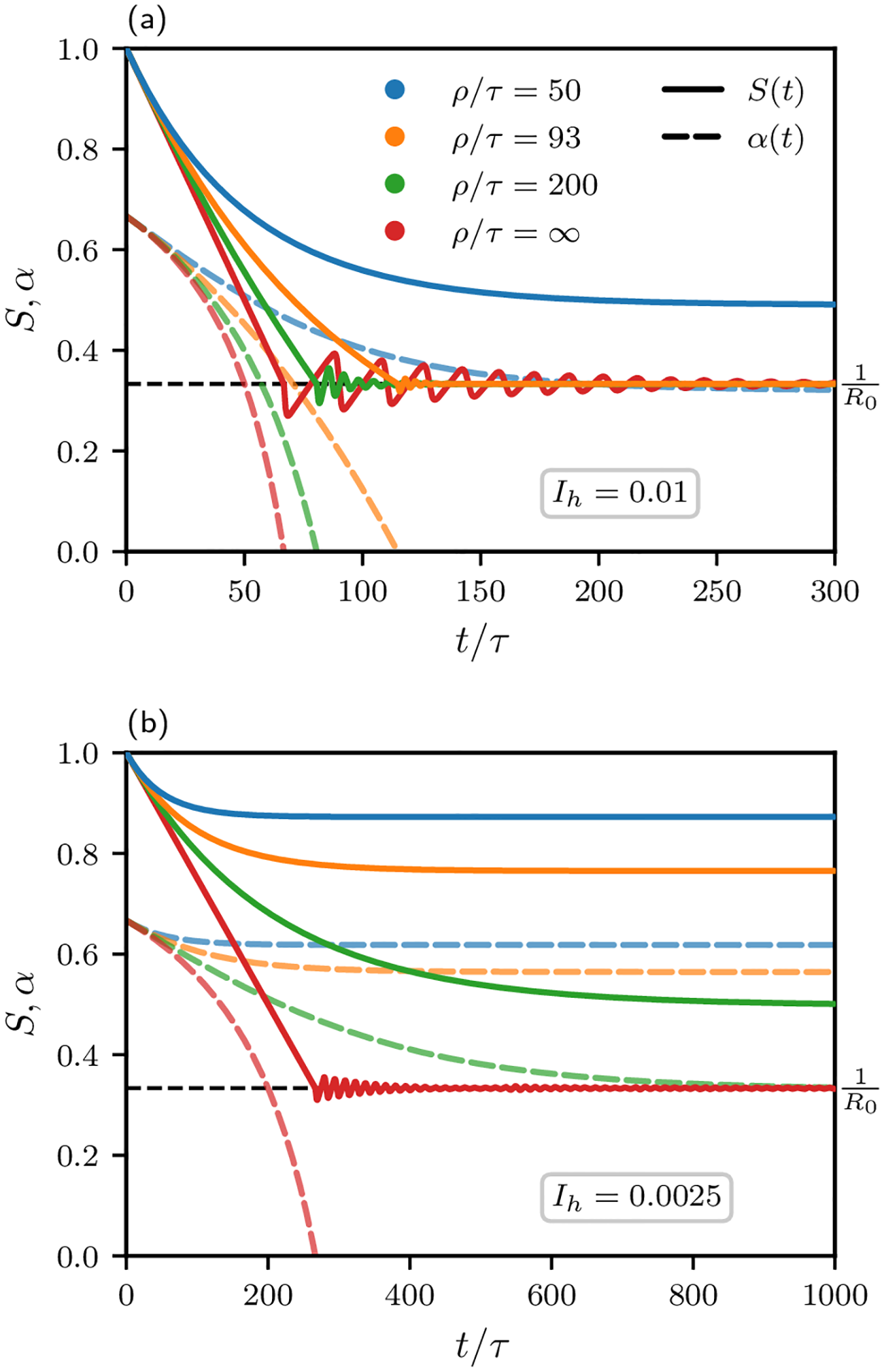
In the framework of homogeneous susceptible-infected-recovered (SIR) models, we use a control theory approach to identify optimal pandemic mitigation strategies. We derive rather general conditions for reaching herd immunity while minimizing the costs incurred by the introduction of societal control measures (such as closing schools, social distancing, lockdowns, etc.), under the constraint that the infected fraction of the population does never exceed a certain maximum corresponding to public health system capacity. Optimality is derived and verified by variational and numerical methods for a number of model cost functions. The effects of immune response decay after recovery are taken into account and discussed in terms of the feasibility of strategies based on herd immunity.

Godara, P.; Herminghaus, S.; Heidemann, K. M.

PLoS One 16 (2), e0247445 (2021)

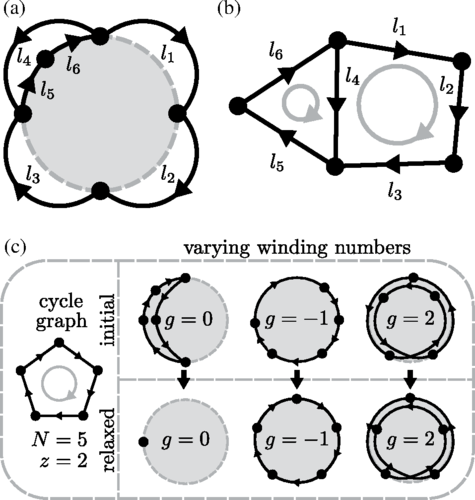
Filamentous polymer networks govern the mechanical properties of many biological materials. Force distributions within these networks are typically highly inhomogeneous, and, although the importance of force distributions for structural properties is well recognized, they are far from being understood quantitatively. Using a combination of probabilistic and graph-theoretical techniques, we derive force distributions in a model system consisting of ensembles of random linear spring networks on a circle. We show that characteristic quantities, such as the mean and variance of the force supported by individual springs, can be derived explicitly in terms of only two parameters: (i) average connectivity and (ii) number of nodes. Our analysis shows that a classical mean-field approach fails to capture these characteristic quantities correctly. In contrast, we demonstrate that network topology is a crucial determinant of force distributions in an elastic spring network. Our results for 1D linear spring networks readily generalize to arbitrary dimensions.

Heidemann, K. M.; Sageman-Furnas, A. O.; Sharma, A.; Rehfeldt, F.; Schmidt, C. F.; Wardetzky, M.

Physical Review Letters 120 (6), 068001 (2018)